odd even trig identities | odd and even identities

Keno, Australia's Number 1 Keno site. Government approved and secure so you can play all your favourite Keno games with confidence.

odd even trig identities*******Finding Even and Odd Identities . 1. Find \(\sin x\) If \(\cos(−x)=\dfrac{3}{4}\) and \(\tan(−x)=−\dfrac{\sqrt{7}}{3}\), find \(\sin x\). We know that sine is odd. Cosine is even, so \(\cos x=\dfrac{3}{4}\). Tangent is odd, so \(\tan .The Even-Odd (or Negative Angle) Identities relate the value of a .The Even / Odd Identities are readily demonstrated using any of the ‘common .Learn how to use the evenness or oddness of trig functions to find values of negative angles. See definitions, examples, and proofs of even and odd identitie.

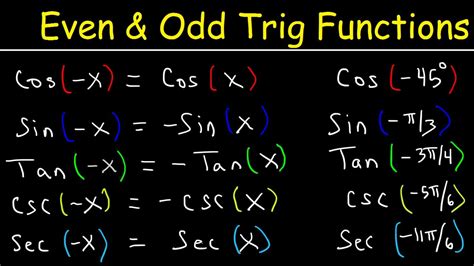
Trigonometric functions are examples of non-polynomial even (in the case of cosine) and odd (in the case of sine and tangent) functions. The properties of even and odd functions are useful in analyzing . This trigonometry video explains how to use even and odd trigonometric identities to evaluate sine, cosine, and tangent trig functions.

Even Odd Trig Identities: The concept of even odd trig identities is an essential aspect of trigonometry, enabling the simplification and manipulation of . The Even-Odd (or Negative Angle) Identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle .odd and even identitieshow to determine whether a Trigonometric Function is Even, Odd or Neither, Cosine function, Secant function, Sine function, Cosecant function, Tangent function, and Cotangent function, How to use the .

Understanding Even Odd Identities. Understand how to work with even and odd trig identities in this free math tutorial video by Mario's Math Tutoring. .more. The Even / Odd Identities are readily demonstrated using any of the ‘common angles’ noted in Section 10.2. Their true utility, however, lies not in .Trig Even-Odd Identities. For angle θ at which the functions are defined: (1) sin ( −θ) = − sin ( θ) (2) cos ( −θ) = cos ( θ) (3) tan ( −θ) = − tan ( θ) (4) cot ( −θ) = − cot ( θ) (5) sec ( . Understand how to work with even and odd trig identities in this free math tutorial video by Mario's Math Tutoring.0:15 Which Functions are Even or Odd1:58 S.The Odd-Even Identities cos ( x ) is an even function, sin ( x ) is an odd function as trigonometric functions for real variables.

The following table shows the Even Trigonometric Functions and Odd Trigonometric Functions. Scroll down the page for more examples and step by step solutions. Even Trigonometric Functions And Identities. .In this first section, we will work with the fundamental identities: the Pythagorean Identities, the even-odd identities, the reciprocal identities, and the quotient identities. We will begin with the Pythagorean Identities (see Table 1 ), which are equations involving trigonometric functions based on the properties of a right triangle. The Even / Odd Identities are readily demonstrated using any of the ‘common angles’ noted in Section 10.2. Their true utility, however, lies not in computation, but in simplifying expressions involving the circular functions. In fact, our next batch of identities makes heavy use of the Even / Odd Identities.All functions, including trig functions, can be described as being even, odd, or neither. A function is odd if and only if f(-x) = - f(x) and is symmetric with respect to the origin. A function is even if and only if f(-x) = f(x) and is symmetric to the y axis. It is helpful to know if a function is odd or even when you are trying to simplify an expression when the .Trig identities. Trigonometric identities are equations that are used to describe the many relationships that exist between the trigonometric functions. Among other uses, they can be helpful for simplifying trigonometric expressions and equations. The following shows some of the identities you may encounter in your study of trigonometry.Example Problem 2 - Proving Trigonometric Identities Using Odd & Even Properties. Step 1: Identify the given trigonometric equation. Step 2: Apply odd and even properties of trigonometric . The Pythagorean identities are based on the properties of a right triangle. cos2θ + sin2θ = 1. 1 + cot2θ = csc2θ. 1 + tan2θ = sec2θ. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle. tan( − θ) = − tanθ. cot( − θ) = − cotθ. The Pythagorean identities are based on the properties of a right triangle. cos2θ + sin2θ = 1. 1 + cot2θ = csc2θ. 1 + tan2θ = sec2θ. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle. tan(− θ) = − tan θ. cot(− θ) = − cot θ.In this first section, we will work with the fundamental identities: the Pythagorean Identities, the even-odd identities, the reciprocal identities, and the quotient identities. We will begin with the Pythagorean Identities (see Table 1 ), which are equations involving trigonometric functions based on the properties of a right triangle.In this explainer, we will learn how to use cofunction and odd/even identities to find the values of trigonometric functions. We have seen a number of different identities and properties for the trigonometric functions that we can use to help us simplify and solve equations. Before we see how we can apply these properties and identities, we .odd even trig identities odd and even identitiesThe following is a list of useful Trigonometric identities: Quotient Identities, Reciprocal Identities, Pythagorean Identities, Co-function Identities, Addition Formulas, Subtraction Formulas, Double Angle .odd even trig identitiesThe trigonometric half-angle identities state the following equalities: The plus or minus does not mean that there are two answers, but that the sign of the expression depends on the quadrant in which the angle resides. . Even-odd identities. The functions , , , and are odd, while and are even. In other words, the six trigonometric functions .

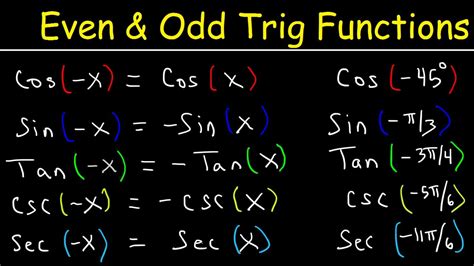
www.mathwords.com. about mathwords. website feedback. Odd/Even Identities. Plus/Minus Identities. Trig identities which show whether each trig function is an odd function or an even function. Odd/Even Identities. sin (– x) = –sin x. cos (– x) = cos x. Recall that we determined which trigonometric functions are odd and which are even. The next set of fundamental identities is the set of even-odd identities. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle (Table \(\PageIndex{2}\)).

Trig Even-Odd Identities For angle θ at which the functions are defined: (1) sin .Lately you've been covering trig functions and the unit circle. As it turns out, trig functions of certain angles are pretty easy to remember. . Even and Odd Identities. An even function is a function where the value of the function acting on an argument is the same as the value of the function when acting on the negative of the argument. Or .

The city of Dubai is the largest and most populated city in the United Arab Emirates (UAE) and the capital city of the emirate of Dubai, UAE.The city is sometimes called "Dubai City" to prevent it from being mixed up with .

odd even trig identities|odd and even identities